مشاكل التصنيف
مشاكل التصنيف شائعة جدًا في مجال التعلم الآلي. كما نعلم في التصنيف، نحاول التنبؤ بتسمية الفئة من خلال دراسة المدخلات (input data) أو المتنبئ (Predictor) حيث يكون الهدف (Target) أو المخرجات (Output data) متغيرًا فئويًا (Categorical Varieble) في الطبيعة.
من تعامل مع نماذج التصنيف، حتما واجه مشكلة البيانات غير المتوازنة حيث أنّها تعتبر من المشاكل الشائعة جدًا في سيناريوهات التصنيف وغالبًا ما يؤدي أي نهج معتاد وعام لحل هذا النوع من مشكلات التعلم الآلي إلى نتائج غير مناسبة.
على سبيل المثال، كشف الاحتيال في الخدمات المصرفية، أو المزايدة بوقت مباشر في التسويق أو اكتشاف التسلل في الشبكات؛ فغالبًا ما تحتوي البيانات المستخدمة في هذه المجالات على أقل من 1٪ من الأحداث (Events) المثيرة للانتباه النادرة، مثل الاحتيال ببطاقات الائتمان، أو النقر على إعلان.
في هذه المقالة، سنناقش مجموعة البيانات غير المتوازنة، والمشاكل المتعلقة بالتنبؤ فيها، وكيفية التعامل مع هذه البيانات و تدريب المصنف على اكتشاف الصنف غير الطبيعي بشكل أكثر كفاءة من الطرق التقليدية والمُعدّة مسبقًا.
ما هي البيانات غير المتوازنة
تشير البيانات غير متوازنة إلى تلك الأنواع من مجموعات البيانات حيث يكون توزيع الفئات غير متساوٍ بناءً على عدد العينات في كل فئة من فئات مجموعة البيانات (observations)، أي أن تصنيف أحد الفئات يحتوي على عدد كبير جدًا من المشاهدات والآخر يحتوي على عدد قليل جدًا من المشاهدات.

التعامل مع البيانات غير المتوازنة
لنفرض أنَّ مصرفًا ماليًّا ما لديه خدمة إصدار بطاقة ائتمان لعملائه. يساور القلق إداريي المصرف بسبب وجود بعض المعاملات الاحتيالية. عند التحقق من بيانات الإحصاء الدورية، تم تسجيل 30 معاملة احتيال لكل 2000 معاملة. فإنَّ نسبة عمليات الاحتيال تقريبًا 2٪، و98٪ معاملة سليمة. بناءً على هذه النسب، تعتبر فئة “لا يوجد احتيال” هي فئة الأغلبية، وفئة “احتيال” هي فئة الأقلية.

المزيد من الأمثلة على البيانات غير المتوازنة
- تشخيص الأمراض
- الكشف عن الغش أو عمل غير مشروع
- التنبؤ بكارثة طبيعية
مشاكل تصنيف البيانات غير المتوازنة
من الطبيعي أن يكون هناك فئات غير متوازنة عند إنشاء نماذج التصنيف. ولكن يكون هذا الخلل حادًا للغاية في بعض الأحيان حيث يكون نسبة فئة الأغلبية أعلى بكثير من نسبة فئة الأقلية.
المشكلة الرئيسية في التنبؤ غير المتوازن لمجموعة البيانات هي مدى صحة التنبؤ (Accuracy) في الواقع لفئة الأغلبية والأقلية. دعونا نشرحها بمثال لتشخيص المرض. لنفترض أننا سنتوقع المرض من خلال مجموعة بيانات حيث تم تشخيص 5 مرضى بالمرض لكل 100 حالة. لذا، فإن نسبة فئة الأغلبية هي 95٪ سليم وفئة الأقلية 5٪ فقط مصاب. الآن، نفترض أن نموذج التصنيف يتنبأ 100 من كل 100 حالة بتشخيص سليم -غير مصاب. عندما تكون عينات فئة معينة أكثر بكثير من عينات الفئة الأخرى في مجموعة البيانات، قد ينحاز نموذج التصنيف بالتنبؤ وينتج عن ذلك نتائج غير واقعية.
طرق التعامل مع مشكلة مجموعة البيانات غير المتوازنة
في حالات نادرة مثل كشف الاحتيال أو تشخيص الأمراض، من الضروري تحديد فئات الأقلية بشكل صحيح. لذلك لا ينبغي أن يكون النموذج متحيزًا لاكتشاف فئة الأغلبية فقط، وإنما يجب أن يعطي وزناً وأهمية متساويتين تجاه فئة الأقلية أيضًا.
سنناقش 7 تقنيات للتعامل مع مجموعات البيانات غير المتوازنة. من المهم التنويه على أنه لا توجد طريقة صحيحة أو طريقة خاطئة من هذه الطرق، فكل مجموعة بيانات تناسبها تقنية مختلفة عن الأخرى.
1. استخدم مقاييس التقييم الصحيحة
مصفوفة الالتباس
مصفوفة الالتباس (Confusion matrix) هي مصفوفة ثنائية الأبعاد تقيس مدى جودة نماذج التصنيف تبعًا لعينات الهدف (Target). حيث يتم تقسيم العدد الإجمالي للتنبؤات الصحيحة بواسطة النموذج على العدد الإجمالي للتنبؤات.
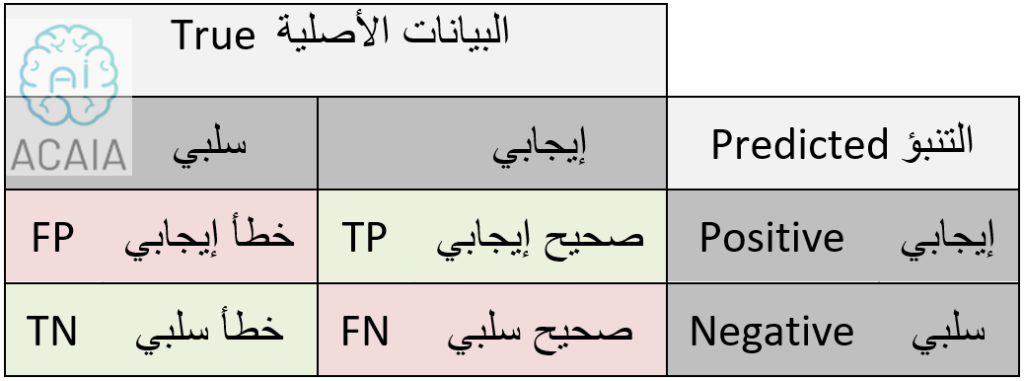
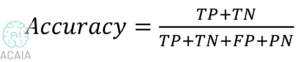
صحة المصنف (Accuracy) هي العدد الإجمالي للتنبؤات الصحيحة بواسطة المصنف مقسومًا على العدد الإجمالي للتنبؤات. قد يكون هذا جيدًا بما يكفي لفصل متوازن، ولكنه ليس مثاليًا لمشكلة الفئات غير المتوازنة. في حال طبقنا الدالة على حالة كشف المرض، فإنّ (0+95) / (0+95+0+5) =0.95 أو 95٪. مما يعني أن النموذج فشل في تحديد فئة الأقلية، ولكن درجة صحة النموذج ستكون 95٪. وبالتالي فإن نهجنا التقليدي في التصنيف وحساب دقة النموذج ليس مفيدًا في حالة مجموعة البيانات غير المتوازنة. المقاييس الأخرى مثل الدقة Precision هي مقياس مدى دقة تنبؤ المصنف لفئة معينة.
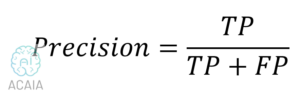
بالنسبة لمجموعة بيانات الفئة غير المتوازنة، تعد النتيجة F1 مقياسًا أكثر ملاءمة. وهي الوسط التوافقي للدقة والاستدعاء وهي حاصل ضرب الدقة بالاستدعاء باثنين قسمة مجموع الدقة والاستدعاء.
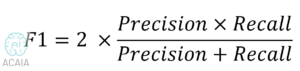
لذلك، إذا توقع المصنف فئة الأقلية، ولكن التنبؤ خاطئ وزيادات التصنيف الإيجابي الخاطئ، فسيكون مقياس الدقة منخفضًا وكذلك درجة F1. وإذا كان المصنف يحدد فئة الأقلية بشكل سيئ، أي أن عددًا أكبر من هذه الفئة تم توقعه بشكل خاطئ على أنه فئة الأغلبية، فسيزيد التصنيف السلبي الخاطئ، لذلك ستنخفض درجة الاستدعاء وستكون درجة F1 منخفضة. تزيد درجة F1 فقط إذا تحسن كل من عدد وجودة قيم التنبؤ.
تحافظ درجة F1 على التوازن بين الدقة والاستدعاء وتحسن النتيجة فقط إذا حدد المصنف قيم أكثر من فئة معينة بشكل صحيح.
2. إعادة أخذ عينات من مجموعة التدريب
يوجد طريقتان لإنشاء واستخلاص مجموعة بيانات متوازنة من مجموعة بيانات غير متوازنة؛ وهما تقليص العينات (Undersampling) وتكثيف العينات (Oversampling).
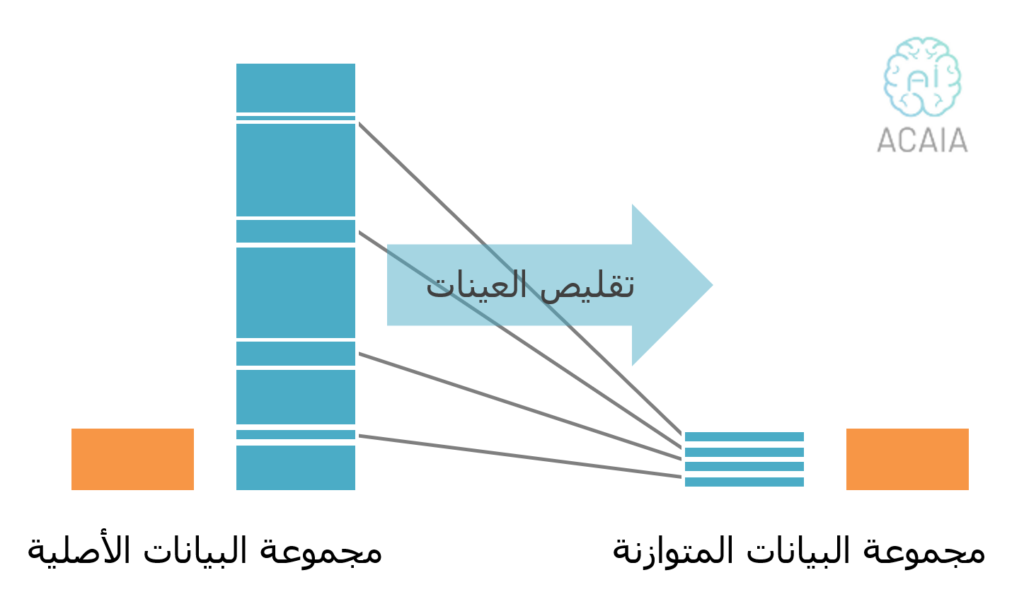
2.1 تقليص العينات
تتم موازنة عينات مجموعة البيانات عن طريق تقليص حجم الفئة الوفيرة (تقليل العينات). تُستخدم هذه الطريقة عندما تكون كمية البيانات كافية. من خلال الاحتفاظ بجميع عينات الفئة النادرة واختيار عشوائي لعدد متساوٍ من عينات الفئة الوفيرة، يمكن استرداد مجموعة بيانات جديدة متوازنة لمزيد من النمذجة.
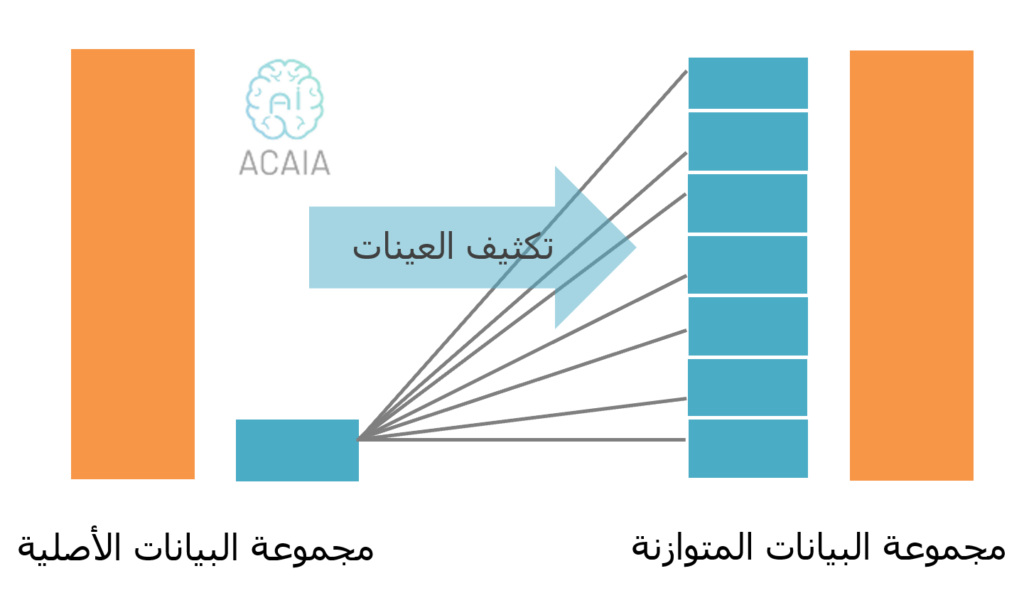
2.2 تكثيف العينات
وعلى عكس التقليص، يتم استخدام تكثيف العينات (زيادة العينات) عندما تكون كمية البيانات غير كافية. يتم موازنة مجموعة البيانات عن طريق زيادة حجم العينات النادرة. بدلاً من التخلص من عينات الفئة الوفيرة، يتم إنشاء عينات نادرة جديدة باستخدام أحد التقنيات مثل التكرار أو التمهيد.
الملاحظ هنا هو أنه لا توجد ميزة مطلقة لطريقة إعادة التشكيل على الأخرى، بل يعتمد تطبيق هاتين الطريقتين على حسب حالة الاستخدام التي تنطبق عليها ومجموعة البيانات نفسها. غالبًا ما يكون الجمع بين تكثيف العينات وتقليص العينات ناجحًا أيضًا.
3. استخدام التحقق المتقاطع على أجزاء (K-fold Cross validation) بالطريقة الصحيحة
إذا تم تطبيق التحقق المتقاطع بعد عملية تكثيف العينات، فإن ما نقوم به في الأساس هو تعديل نموذجنا إلى نتيجة تشغيل اصطناعية (Artificial Bootstrapping ) محددة. ولذلك يتحتم إجراء التحقق المتقاطع دائمًا قبل تكثيف العينات، تمامًا مثل كيفية تنفيذ اختيار الصفات المهمة (Features). فقط من خلال إعادة تجميع البيانات بشكل متكرر، يمكن أيضًا تطبيق العشوائية في مجموعة البيانات للتأكد من عدم وجود مشكلة تغذية فائضة (Overfitting).
4. تجميع مجموعات البيانات المستنسخة المختلفة
أسهل طريقة لتعميم نموذج بنجاح هي استخدام المزيد من البيانات. تكمن المشكلة في المصنفات الجاهزة مثل مصنف الانحدار اللوجستي أو مصنف الغابة العشوائية تميل إلى استراتيجيات معالجة عامة وغير مخصصة ولذلك تقوم بالتخلص من الفئة النادرة.
لحل هذه المشكلة نقوم ببناء نماذج بعدد N تستخدم جميع عينات الفئة النادرة وعينات بعدد N مختلفة من فئة وفيرة. نظرًا لأننا نريد تجميع 10 نماذج، فسنحتفظ ب 1000 حالة من الفئة النادرة وكعينة عشوائية 10000 حالة من الفئة الوفيرة. ثم نقوم فقط بتقسيم 10000 حالة إلى 10 أجزاء ثم القيام بتدريب 10 نماذج مختلفة.
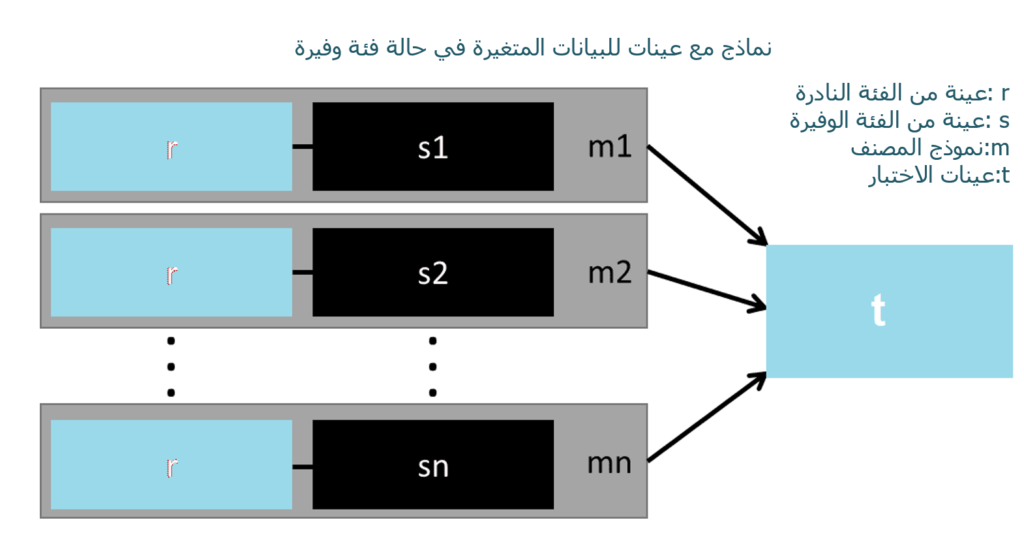
إذا كان لدينا الكثير من البيانات فيعتبر هذا الأسلوب بسيط وقابل للتطوير أفقيًا تمامًا، حيث يمكن فقط تدريب النماذج وتشغيلها على مجموعة مختلفة. تميل نماذج المجموعات أيضًا إلى تطبيق استراتيجيات معالجة البيانات العامة بشكل أفضل، مما يجعل هذا النهج سهل التعامل معه.
5. إعادة أخذ العينات بنسب مختلفة
يمكن صقل النهج السابق من خلال التلاعب بالتناسب بين فئة نادرة وفئة وفيرة. يعتمد أفضل تناسب بشكل كبير على البيانات والنماذج المستخدمة. ولكن بدلاً من تدريب جميع النماذج بنفس النسبة في المجموعة، نقوم بتجميع النسب المختلفة. لذلك إذا تم تدريب 10 نماذج، فقد يكون من المنطقي أن يكون لديك نموذج بنسبة 1: 1 (نادر: متوفر) وآخر به 1:3، أو حتى 2: 1. اعتمادًا على النموذج المستخدم، يمكن أن يؤثر ذلك على الوزن الذي تحصل فئة واحدة عليه.
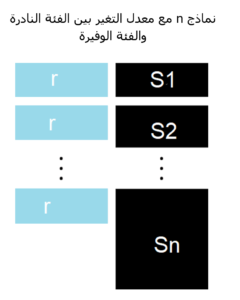
6. مجموعة الصنف الوفير
تم اقتراح نهج بسيط واحترافي من قبل سيرجي على Quora. فبدلاً من الاعتماد على عينات عشوائية لتغطية مجموعة متنوعة من عينات التدريب، يقترح سيرجي تجميع الصنف الوفير في مجموعات r، حيث يكون r هو عدد الحالات فيr. لكل مجموعة، يتم الاحتفاظ فقط بالنقطة المركزية في العينة (medoid)، ثم يتم تدريب النموذج مع فئة نادرة والنقطة المركزية فقط فإذا أخدنا على سبيل المثال عدد العينات N في الفئة النادرة. سنصنف إلى عدد N من المجموعات، ثم نستخدم نسبة قيم النقاط المركزية للمتوسط الحسابي (mediods/means) الناتجة كبيانات تدريب لشعبة الفئة الوفيرة. أولًا علينا التخلص من بيانات التدريب الأصلية من شعبة الفئة الوفيرة، واستبدالها بقيم المتوسط الحسابي (means). وبهذه الطريقة يتم الحصول على فئات متوازنة (شُعَب) ((Classes.
7. تصميم النموذج الخاص بك
تركز جميع الطرق السابقة على البيانات وتحافظ على النماذج كمكون ثابت. ولكن في الواقع، ليست هناك حاجة لتطبيق استراتيجيات إعادة عينة البيانات إذا كان النموذج مناسبًا للبيانات غير المتوازنة.
مراقبة الأخطاء في النموذج وإصلاحها
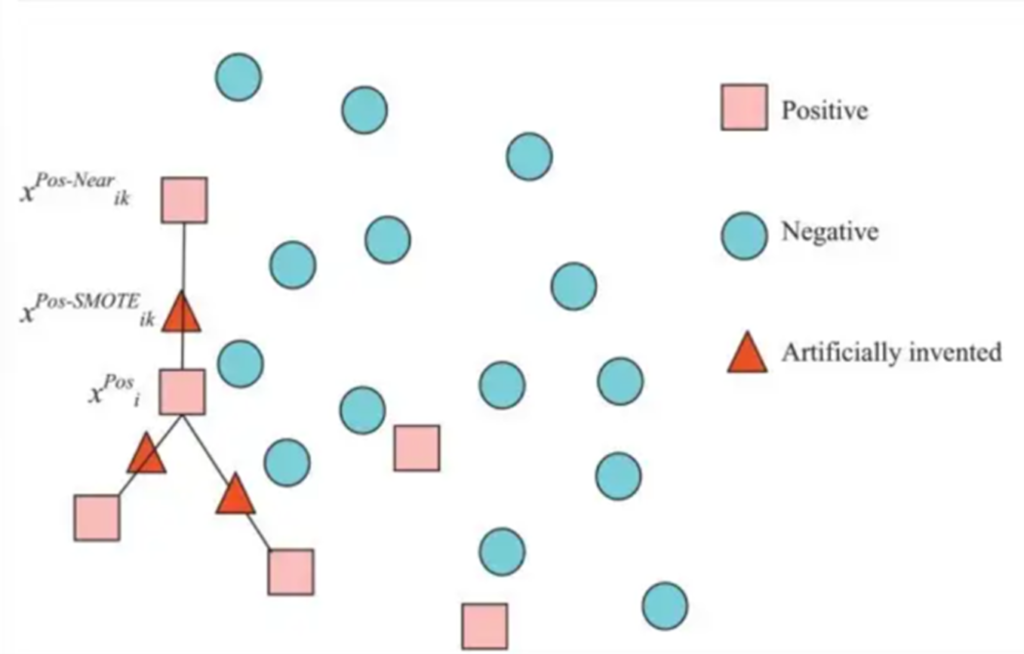
من خلال تصميم دالة التكلفة Cost equation التي تعاقب التصنيف الخاطئ للفئة النادرة أكثر من التصنيفات الخاطئة للفئة الوفرة، من الممكن تصميم العديد من النماذج التي تطبق استراتيجيات معالجة البيانات العامة بشكل طبيعي لصالح الفئة النادرة. مثل استراتيجية تغيير العينات واستراتيجية تبديل العينات في SVM لمعاقبة التصنيفات الخاطئة للفئة النادرة بنفس النسبة التي تكون فيها هذه الفئة ممَثلة تمثيلًا ناقصًا. كذلك يمكننا الحديث عن تقنية تكثيف العينات في الأقليات المصطنعة (SMOTE – Synthetic Minority Oversampling Technique). إن إضافة عينات مكررة لفئة الأقلية غالبًا لا تضيف أي معلومات جديدة إلى النموذج. في SMOTE يتم تصنيع عينات جديدة من البيانات الموجودة. إذا شرحنا ذلك بكلمات بسيطة وكما هو موضح بالرسم، فإنّ SMOTE تركز على حالات فئة الأقليات وتستخدم العدد k لاختيار أقرب جار عشوائي، ويتم إنشاء مثيل اصطناعي عشوائيًا في فضاء الصفات المميزة (Feature space).
خلاصة
هذه ليست قائمة حصرية من التقنيات ، بل هي نقطة انطلاق للتعامل مع البيانات غير المتوازنة. لا يوجد نهج أو نموذج هو الأفضل، بل كل مشكلة ولها تقنية مناسبة، ويوصى بشدة بتجربة تقنيات ونماذج مختلفة لتقييم ما هو الأفضل لمجموعة البيانات والنموذج الخاص بك. حاول أن تكون مبدعًا وتجمع بين الأساليب المختلفة!
المصادر
- www.quora.com/In-classification-how-do-you-handle-an-unbalanced-training-set/answers/1144228?srid=h3G6o
- https://arxiv.org/pdf/1106.1813.pdf
- https://classeval.wordpress.com/introduction/basic-evaluation-measures/#:~:text=Precision%20is%20calculated%20as%20the,predictions%20(TP%20%2B%20FP).
- https://medium.com/analytics-vidhya/handling-imbalanced-classes-3057a88e2a19