مقدمة
المرشحات (Filters) هي تقنية تساعد في تغيير ملامح الصورة أو مواصفاتها، وهي الأساس البرمجي للتقنيات الحديثة التي نشاهدها في التطبيقات الذكية وبرامج التواصل الاجتماعي، وبرامج تعديل الصور الذكية، مثل التطبيقات: تجميل الصورة، وضع مستحضرات تجميل افتراضية، تغيير ألوان المشهد من الصيفية إلى الشتوية، إظهار حدود الكائنات في الصورة، تشويش الصورة، شحذ الصورة. ذلك يتم عن طريق ترشيح الصورة باستخدام نواة الالتفاف (Convolution Kernal) ودالة الالتفاف (Convolution). في هذا المقال تم تطبيق الأنوية والمرشحت باستخدام مكتبة اوبن سي في بلغة بايثون.
الالتفاف والطي:
أيضًا تسمى عملية الالتفاف بعملية الطي، نظرًا لأنه يتم اختزال 9 مربعات بكسل في مربع واحد في الصورة الناتجة، وكأنه طويت، أو تم لفها. فالمعنى يحتمل المصطلحين الطي والالتفاف، لكن الالتفاف هو أقرب للمبدأ العلمي، حيث إنه سمي بذلك بناءً على تشبيهه بخلايا المخ العصبية الالتفافية والتي تتكون من التفافات كثيرة.
المحتويات
سأطرح في هذا المقال المواضيع التالية:
1.نواة الالتفاف وعملية الالتفاف
2.الترشيح والمرشح
3.أشهر الأنوية الحاسوبية والتطبيق عليها
– نواة التطابق (Identity Kernel)
– نواة التشويش (Blur Kernel)
– نواة الشحذ (Sharpening Kernel)
4.أنواع المرشحات
– مرشح سوبل (Sobel) لتحديد الحواف
– مرشح كاني (Canny) لتحديد الحواف
– مرشحات أخرى
5.واجهة جاهزة لتجريب المرشحات بدون برمجة
6.خاتمة
1.نواة الالتفاف وعملية الالتفاف والترشيح والمرشح
لفهم المرشحات أولًا علينا فهم نواة الالتفاف في معالجة الصور
نواة الالتفاف (Convolution Kernel)
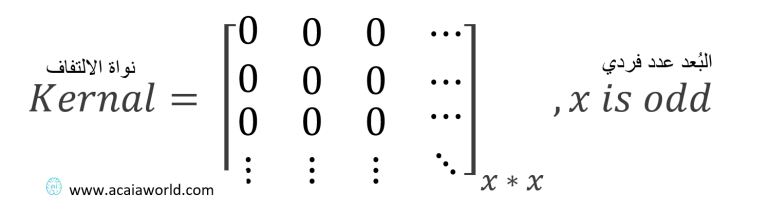
نواة الالتفاف هي مصفوفة ثنائية الأبعاد تتكون من نمط معين من الأرقام. لتوضيح الفكرة أكثر، لنفترض أن نواة الالتفاف هي الثابت ن والصورة هي المصفوفة المتغيرة س. سينتح عن ذلك ن × س = صورة جديدة. عملية ضرب النواة بالصورة تكون على مستوى مربعات بكسل.
النواة هي مصفوفة من الأوزان يتم ضربها بمصفوفة الصورة المدخلة لاستخراج الخواص المميزة. الالتفاف يطلق على العملية كاملة وفي حال كانت مصفوفة النواة ثنائية البعد، سيكون الالتفاف ثنائي البعد.
عملية الالتفاف
عملية الالتفاف هي عملية رياضية بين نواة الالتفاف والصورة وبذلك ينتج ترشيح الصورة. على سبيل المثال، في التفاف ثنائي الأبعاد، المرشحات هي مصفوفات ثلاثية الأبعاد، إذن، لطبقة في الشبكة العصبية الالتفافية مع وجود نواة أبعادها الطول في العرض، بالإضافة إلى بعد قناة الصورة المدخلة، ستكون أبعاد المرشح هي: الطول في العرض في القناة.
والدالة التالية هي دالة الترشيح العامة. حيث إن عملية الالتفاف تتم على المستوى الأفقي والمستوى العامودي للصورة.
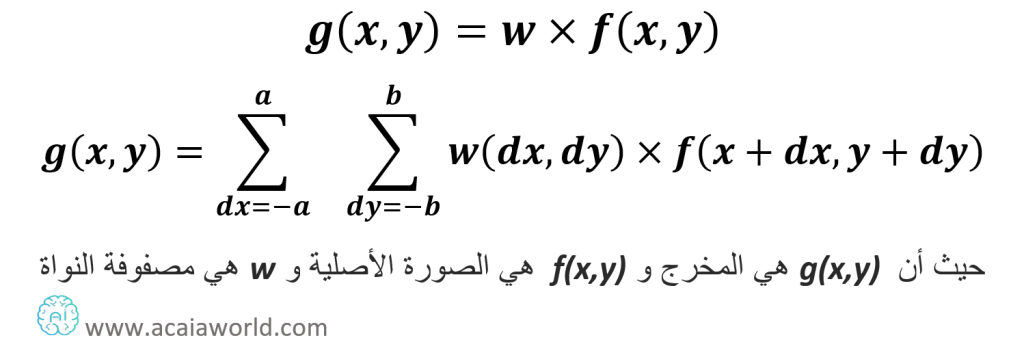
الترشيح والمرشح
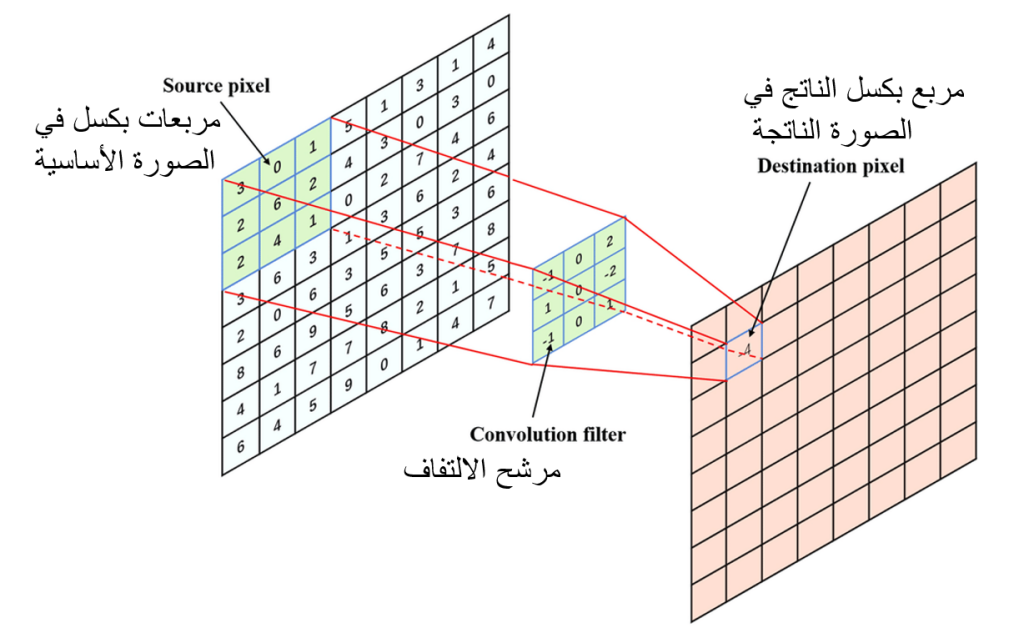
الترشيح هي عملية تطلق على كافة ما سبق وتتكون من الصورة وعدة أنوية وعمليات التفاف حسب الهدف، وتتم عملية الترشيح على المستوى العامودي (الصادي) والمستوى الأفقي ( السيني) ولذلك يتم استخدام أكثر من نواة، من أجل معالجة اختلاف الاتجاهات.
المرشح هو سلسلة متتابعة من عدة أنوية، كل نواة تسند إلى قناة محددة من الصورة المدخلة. المرشح يملك بُعد زائد على النواة دائمًا. وينسب اسم إلى نوع العملية أو اسم مبتكر دالة ونواة الترشيح، فمثلًا يوجد مرشح اسمه لابلاسيال وقد سمي بذلك نسبة إلى مبتكر هذا المرشح. ونواة الالتفاف هي أبسط من المرشح، حيث إن المرشح يحتوي على عدة أنوية التفافية.
الصورة التالية توضح شكل المرشح أو النواة بين الصورة المدخلة وموقع الناتج بعد عملية الترشيح.
3.أشهر الأنوية الحاسوبية والتطبيق عليها
سأذكر في هذا المقال عملية الترشيح باستخدام عدة أنوية
- نواة التطابق
- نواة التشويش
- نواة الشحذ
1.نواة التطابق
نواة التطابق هي مصفوفة مربعة يتوسطها الرقم واحد وبقية العناصر تكون صفرًا، كما هو موضح في المصفوفة x. ما يميز مصفوفة التطابق أنه حينما يتم ضربها بأي مصفوفة ستنتج المصفوفة (الصورة) الأصلية.
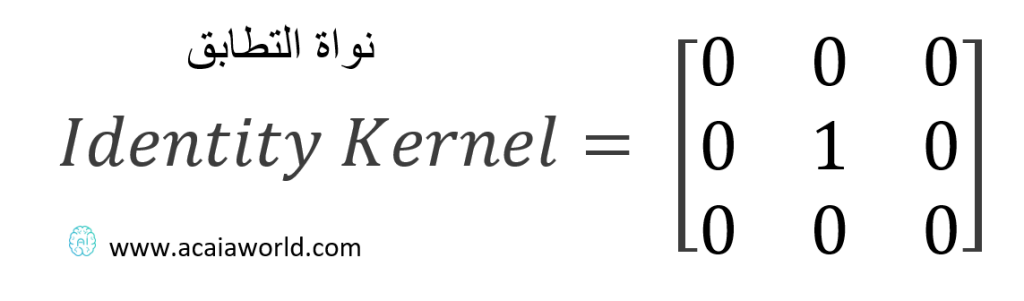
وهذا مثال تطبيقي على ترشيح صورة بنواة التطابق (نواة التفاف التطابق)
النص البرمجي للترشيح بنواة التطابق
image = cv2.imread('test.jpg')
"""
Apply identity kernel
"""
kernel1 = np.array([[0, 0, 0],
[0, 1, 0],
[0, 0, 0]])
# filter2D() function can be used to apply kernel to an image.
# Where ddepth is the desired depth of final image. ddepth is -1 if...
# ... depth is same as original or source image.
identity = cv2.filter2D(src=image, ddepth=-1, kernel=kernel1)
# We should get the same image
cv2.imshow('Original', image)
cv2.imshow('Identity', identity)
cv2.waitKey()
cv2.imwrite('identity.jpg', identity)
cv2.destroyAllWindows()
ناتج الترشيح بنواة التشويش


2.نواة التشويش
يوجد عدة أنوية التفافية للاستخدام المباشر عن طريق اوبن سي في، سنطبق ترشيح الصورة باستخدام نواة مخصصة.
أولًا أنشأنا نواة (5×5)، جميع عناصرها آحاد. ثم قسمنا جميع العناصر على 25. سبب القسمة هو تسوية الصورة وتهيئتها (Normalizing). وتحويل القيم إلى قيمة ما بين الصفر والواحد. الصورة التالية توضح المصفوفة بعد إجراء القسمة عليها.
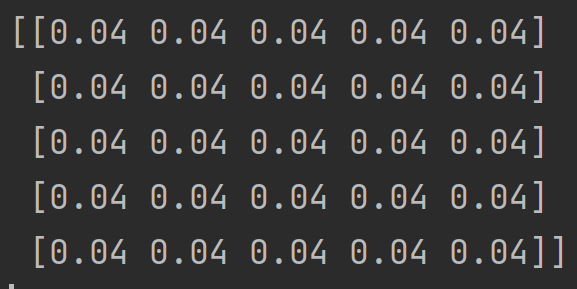
النص البرمجي للترشيح بنواة التشويش
"""
Apply blurring kernel
"""
kernel2 = np.ones((5, 5), np.float32) / 25
img = cv2.filter2D(src=image, ddepth=-1, kernel=kernel2)
cv2.imshow('Original', image)
cv2.imshow('Kernel Blur', img)
cv2.waitKey()
cv2.imwrite('blur_kernel.jpg', img)
cv2.destroyAllWindows()
في السطر الأول من الكود استخدمنا مصفوفة (نواة) ذات البعد 5 × 5 وذلك عن طريق مكتبة NumpPy ثم تقسيم عناصر المصفوفة على 25. وبذلك ينتج المصفوفة الموضحة بالصورة.
ناتج الترشيح بنواة التشويش

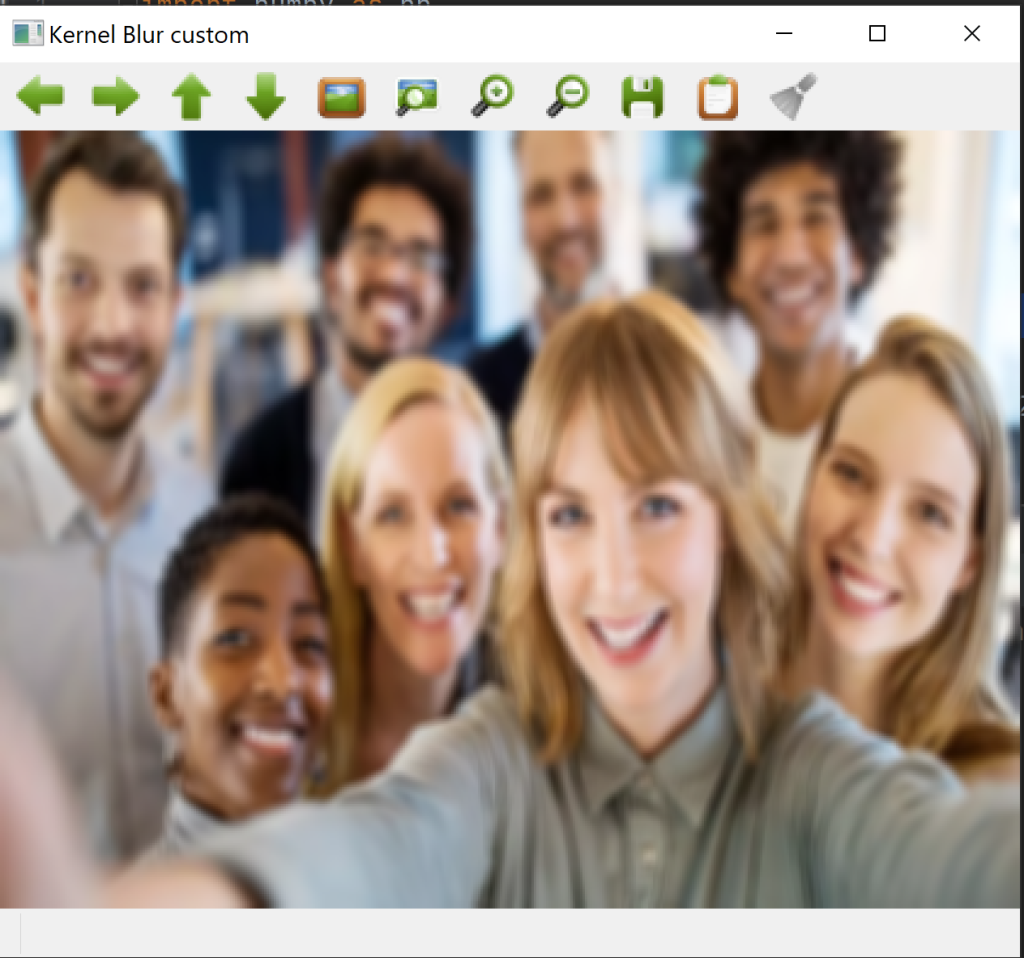
3.نواة الشحذ
شحذ الصورة يعني أن تصبح الصورة ذات طابع حاد أكثر من الأصل. أولًا نبني نواة ثنائية الأبعاد (3×3) ثم نستعين بالدالة الجاهزة filter2D لتطبيق علمية الالتفاف على الصورة.
النص البرمجي للترشيح بنواة الشحذ
"""
Apply sharpening using kernel
"""
kernel3 = np.array([[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]])
sharp_img = cv2.filter2D(src=image, ddepth=-1, kernel=kernel3)
cv2.imshow('Original', image)
cv2.imshow('Sharpened', sharp_img)
cv2.waitKey()
cv2.imwrite('sharp_image.jpg', sharp_img)
cv2.destroyAllWindows()
ناتج الترشيح بنواة الشحذ

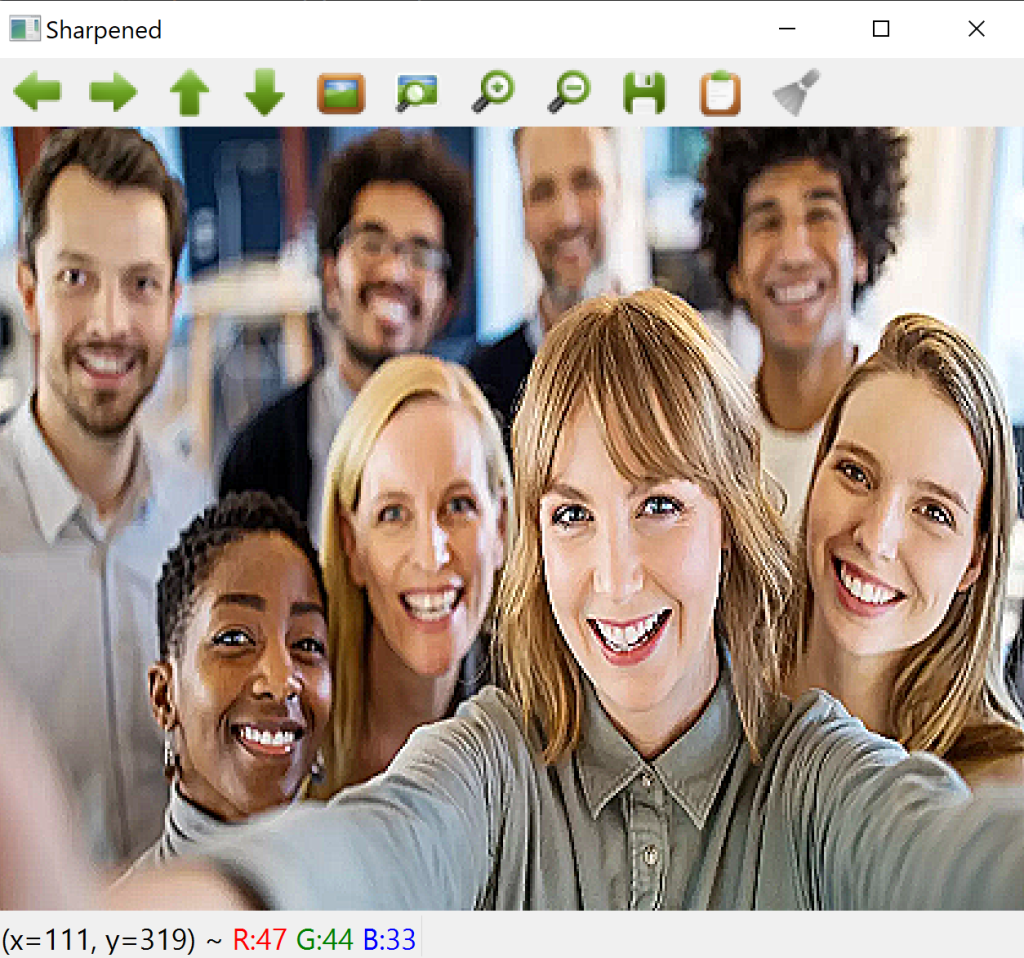
4.أنواع المرشحات
بعد أن انتهينا من ماهية الأنوية وتطبيق عمليات التفاف على بعض الأنوية، ننتقل إلى المرشحات. كما ذكرت سابقًا، الأنوية هي الأساس للمرشح. فالمرشح الواحد يعتمد على عدة أنوية ودوال عتبة، ويكون ذا جودة أعلى ومخرج أفضل وأعقد حسابيًا من النواة المنفردة عند تطبيقها في عملية الترشيح.
وفي هذا المقال سأذكر سبع مرشحات، ولكن سأشرح منها اثنين بالتفصيل مرفقة بالنص البرمجي بلغة بايثون:
- مرشح سوبال (Sobel Filter)
- مرشح كاني لتحديد الحواف (Canny Filter)
- مرشح التشويش القيزي (Gaussian Blur Filter)
- المرشح ثنائي الجوانب (Bilateral Filter)
- مرشح لابلاسيال لتحديد الحواف (Laplacian)
- مرشح التآكل التشكيلي (Morphological Erosion Filter)
- مرشح التمدد التشكيلي (Morphological Dilation Filter)
1. مرشح سوبل لتحديد الحواف
مرشح سوبل هو من المرشحات الأساسية والذي يعمل على رسم الحواف وإلغاء الألوان.
من المهم معرفة حساب التفاضل الاشتقاقات في معالجة الصور. على سبيل المثال في الصورة التالية نستطيع ملاحظة الحواف بشكل مرئي عند الدائرة الحمراء.

يمكنك ملاحظة الحافة عن طريق ملاحظة شدة التغير بألوان مربعات بكسل بشكل طبيعي. يمكننا استخدام حساب الاشتقاقات لإظهار تلك التغيرات بشكل دقيق. التغير القوي في الانحدارات يوضح تغير كبير في الصورة.
لتوضيح شدة التغير بشكل أكبر، يمكننا تمثيل الحافة بشكل مستوى إحداثي (أحادي البعد) وكما هو موضح في الصورة على اليمين في تغير الشدة وتسمى قفزة أو نقلة. ولرؤيتها بشل أوضح كما هو موضح في الصورة على اليسار، في الاشتقاق الأول نلاحظ القفزة بشكل أكبر.

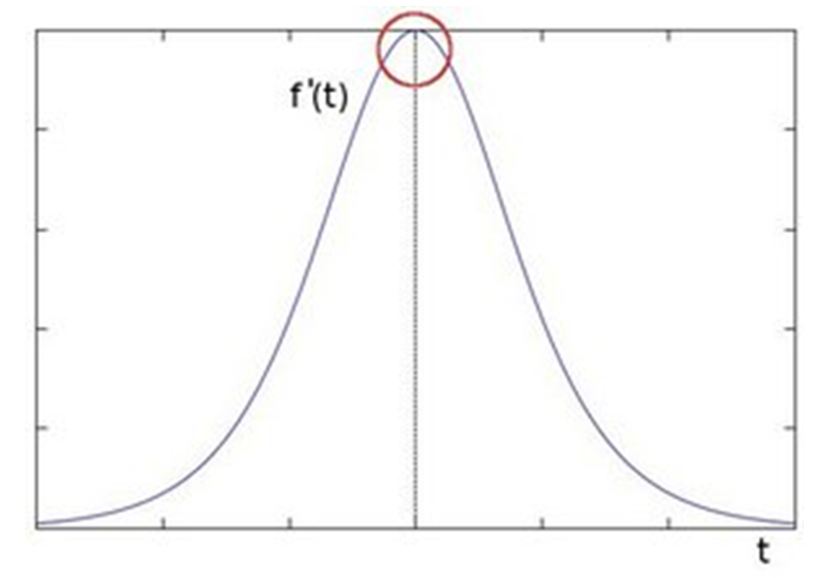
بعد أن تعرفنا على مبدأ تغير الشدة في الحواف، يمكن الاستنتاج بأن تحديد الحواف في الصورة يكون عن طريق تحديد مواقع مربعات بكسل التي يكون فيها الانحدار أعلى من المربعات المحيطة (أعلى من العتبة).
لنفترض أن الصورة التي نريد تطبيق سوبال عليها هي N
أولا نقوم بحساب اشتقاقين:
- التغير الأفقي: وذلك يتم عن طريق تطبيق عملية الالتفاف بين الصورة (N) ونواة (Gx) من قياس من فردي (3×3، 5×5، 7×7، …).
- التغير العمودي: وذلك يتم عن طريق تطبيق عملية الالتفاف بين الصورة (N) ونواة (Gy). وتكون النواة بنفس قياس نواة (Gx).
الصورة التالية توضح نواة سوبل الأفقية ونواة سوبال العمودية المستخدمتين في دوال اوبن سي في وعملية الالتفاف بينها وبين الصورة (N) :

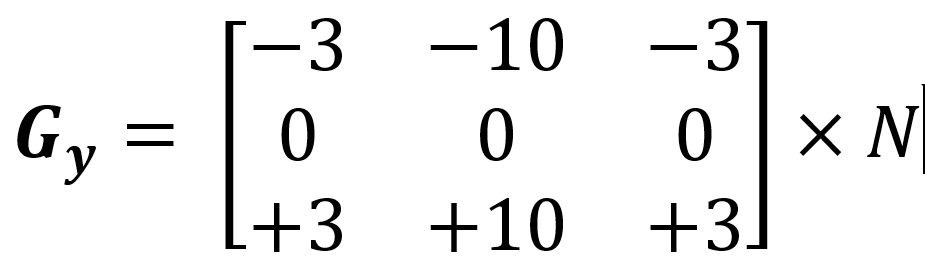
يتم تطبيق الدالة التالية لحساب الانحدار في كل مربع بكسل في الصورة:
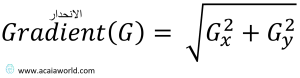
بعد حساب الانحدار يمكن تقريب زاوية الانحدار تبعًا للدالة التالية:
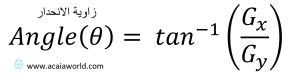
لتطبيق مرشح سوبل على الصورة أولًا يجب أن يتم تحويلها إلى صورة بمساحة اللون الرمادي.
النص البرمجي لعملية الترشيح بمرشح سوبل
import cv2
image = cv2.imread(' /test.jpg')
image = cv2.resize(image, (420,320))
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
ret,binary = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU | cv2.THRESH_BINARY_INV)
grad_x = cv2.Sobel(binary, cv2.CV_8U, dx=0, dy=1, ksize=3)
grad_y = cv2.Sobel(binary, cv2.CV_8U, dx=1, dy=0, ksize=3)
grad = cv2.addWeighted(grad_x, 0.5, grad_y, 0.5, 0)
cv2.imshow('gray image', gray)
cv2.imshow('Sobel gradient X',grad_x)
cv2.imshow('Sobel gradient Y',grad_y)
cv2.imshow('Sobel Image Gx and Gy',grad)
cv2.waitKey()
ناتج تحويل الصورة إلى صورة بدرجات اللون الرمادي

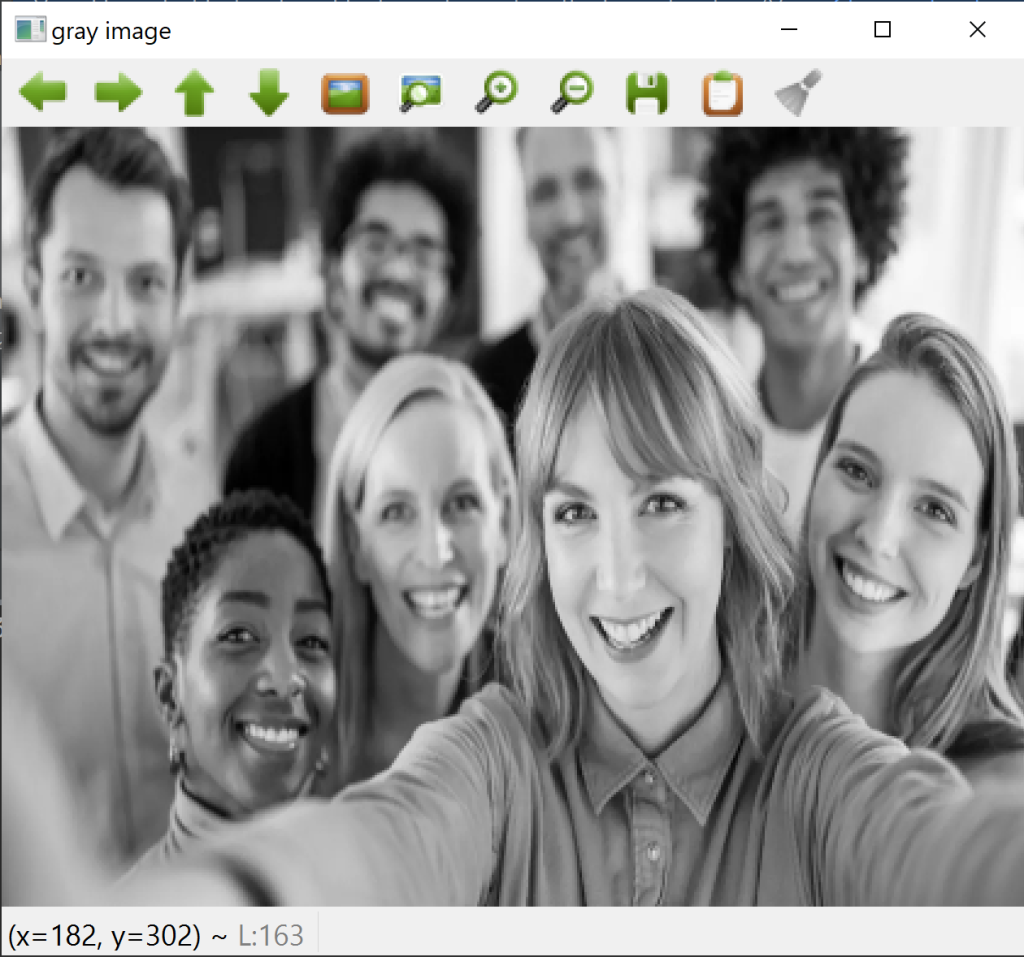
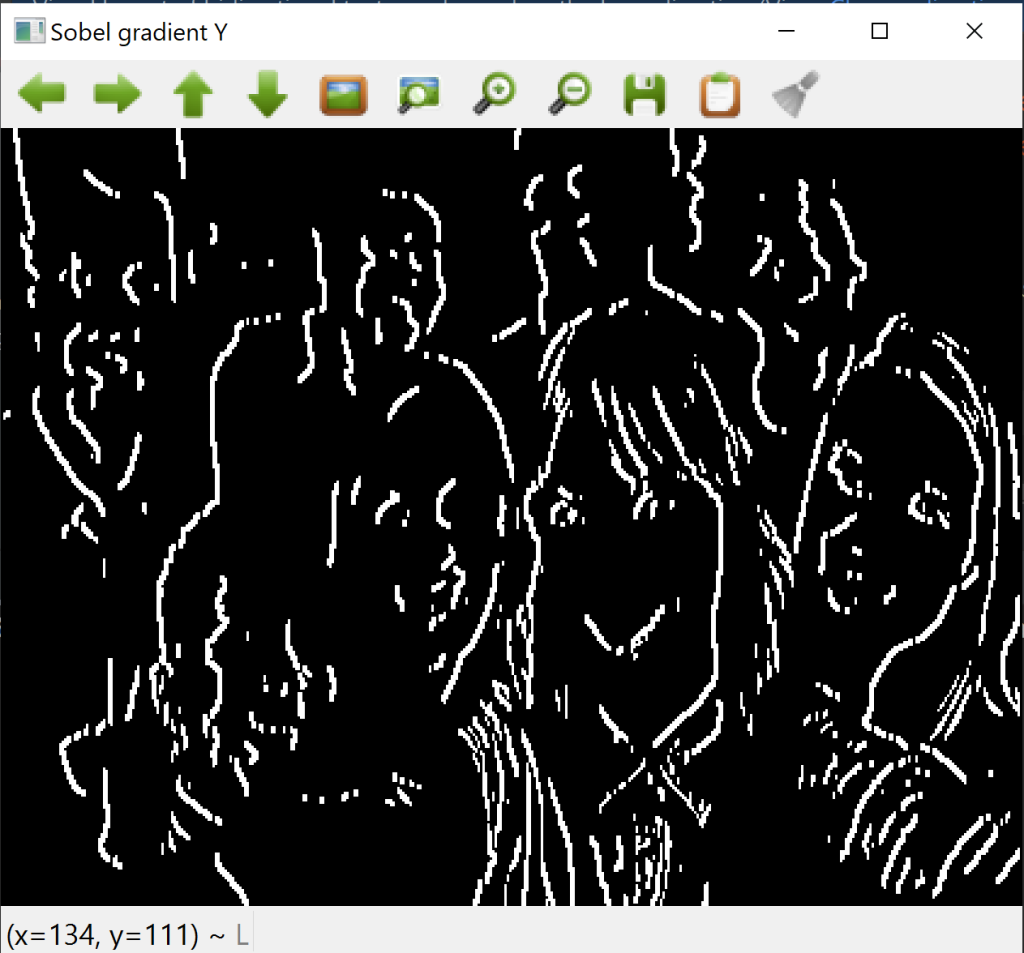
نواتج الترشيح بمرشح سوبل
المستوى العمودي
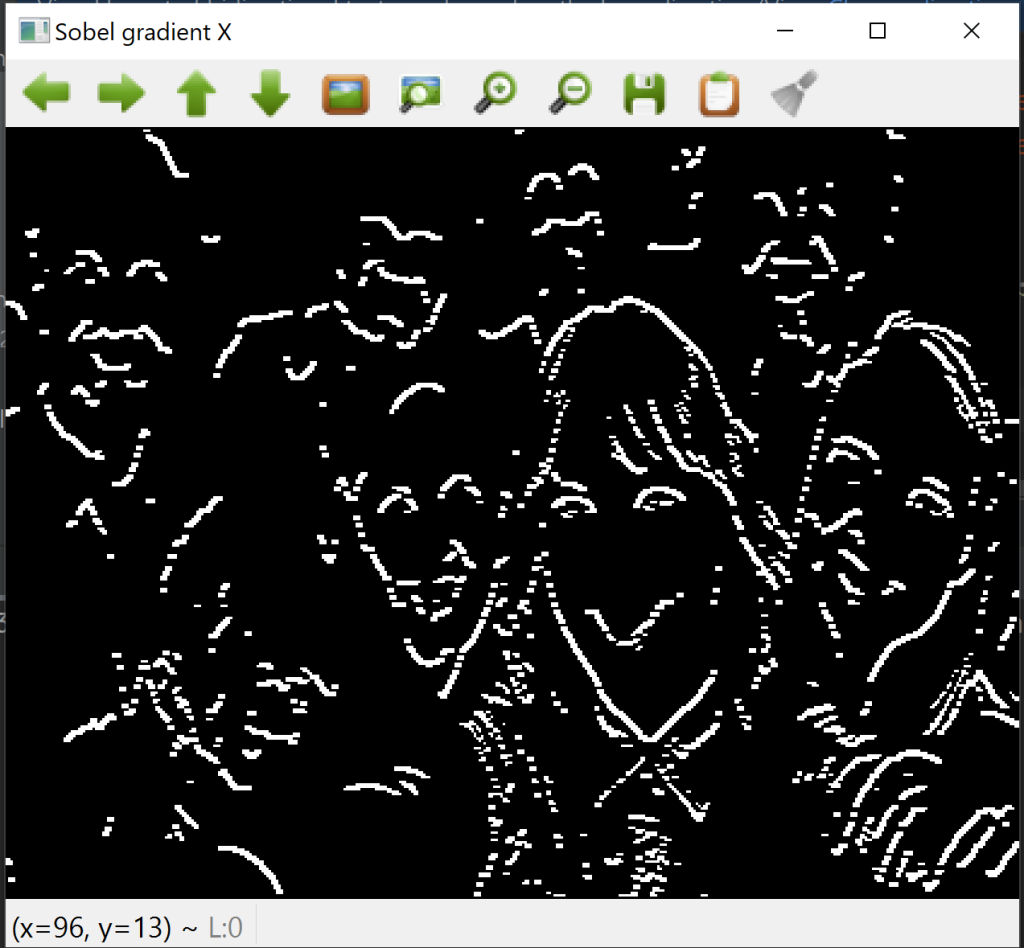
المستوى الأفقي
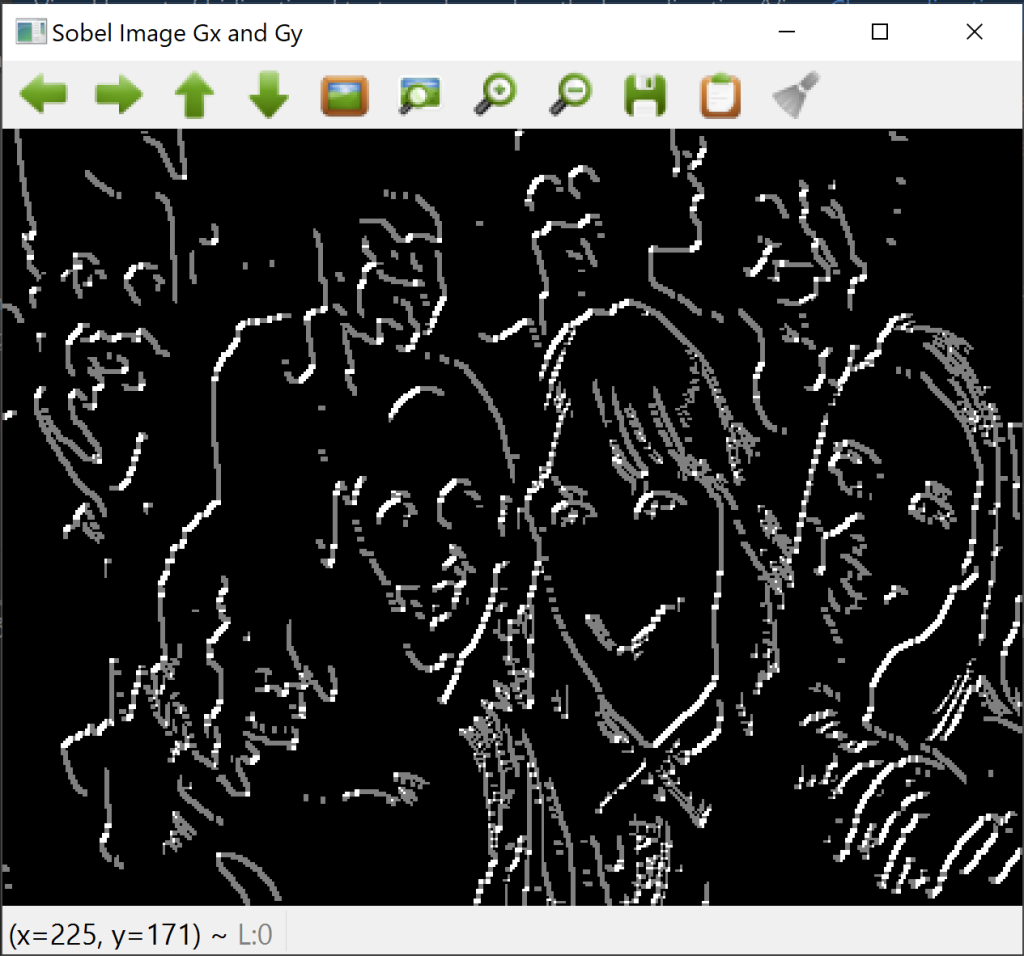
المرشح كامل
2. مرشح كاني لتحديد الحواف (Canny Filter)
مرشح كاني من أشهر المرشحات لإيجاد حدود الكائنات، فهو يعمل على إيجاد الانحدارات بشكل أذكى من سوبل. وذلك عن طريق عدة أنوية للمستوين الأفقي والعمودي والميل. وتعود تسميته بذلك إلى مطوره جون كاني وهو يتكون من عدة مراحل:
1. تقليص الضوضاء
بما أن تحديد الحواف معرض جدًا للضوضاء في الصورة، الخطوة الأولى هي إزالة الضوضاء في الصورة بواسطة فلتر قيزيان (5×5).
2. إيجاد حدة الانحدار
الصورة الناتجة عن العملية الأولى (الصورة المملسة) يتم ترشيحها بنواة سوبل على المستويين(G) الأفقي والعمودي. يمكننا إيجاد انحدار الحواف واتجاه كل بكسل، كما تم تفصيله في فقرة مرشح سوبال.
3. خزل الانحدارات
بعد استنتاج شكل واتجاه الانحدارات، يتم إزالة مربعات بكسل التي لا تشكل الحواف. تتم عملية الإزالة عن طريق فحص كل بكسل، في حال كان انحدار أقصى محلي بين مربعات بكسل المحيطة بمعيار اتجاه الانحدارات، كما هو موضح بالصورة التالية:
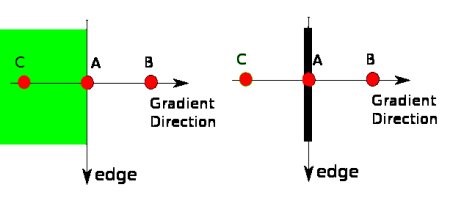
النقطة (A) تقع على الحافة (في الاتجاه الأفقي). اتجاه الانحدار طبيعي بالنسبة إلى الحافة. النقاط (B) و (C) يقعان في اتجاهات الانحدار. إذن، النقطة (A) تم فحصها بالنقاط (B) و (C). لفحص إذا كانت تشكل انحدار أقصى محلي، حينها يتم اعتبارها للمرحلة التالية، وإلا يتم إقصاؤها. النتيجة ستكون صورة بالأبيض والأسود تشكل حدود رفيعة.
4. نظام العتبة الهستيري
في هذه المرحلة، يقرر نظام العتبة في حال كانت كل الحواف حواف حقيقية أم لا. لتطبيق هذا الشرط، نحتاج إلى قيم عتبة، القيمة العظمى، والقيمة الدنيا. أي حواف تملك انحدار شديد أعلى من العتبة العظمى هي حواف حقيقية، في حين أي حواف تحت العتبة الدنيا هي ليست حواف ويتم إقصاؤها. القيم التي تكون بين العتبتين يتم تصنيفها كحواف أو انحدارات أخرى بناءً على ترابط تلك القيم. في حال كانت الحواف مرتبطة بمربعات بكسل التي تملك حواف حقيقية، تعتبر أجزاء من تلك الحواف. وفي حال كانت غير ذلك يتم إقصاؤها، كما هو موضح في الصورة التالية:
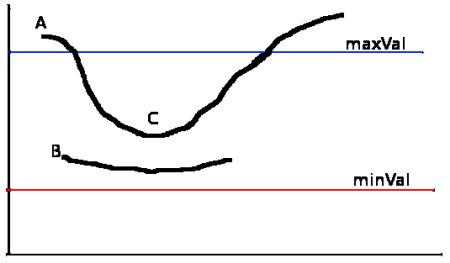
الحافة (A) تقع فوق العتبة العظمى، وبناء على ذلك تم اعتبارها حافة حقيقية. بالرغم من وقوع الحافة (C) تحت العتبة العظمى فهي تعتبر حافة حقيقية نظرًا لاتصالها بالحافة (A) ويشكل الانحدار الذي يقع على النقاط (A) و(C) منحنى كامل. في حين أن الحافة (B)، بالرغم من أنها تقع فوق العتبة الدنيا (نفس منطقة الحافة C)، فهي ليست متصلة مع أي حافة حقيقية، وبناءً على ذلك يتم إقصاء الحافة (B).
3. مرشحات أخرى
- مرشح التشويش القيزي
وهو نوع أفضل من مرشحات التشويش يقوم بتطبيق دالة المسافة القيزية إضافة إلى نواة التشويش
- المرشح ثنائي الجوانب (Bilateral Filter)
هو مرشح ثنائي الأبعاد، يتميز بالحفاظ على الحواف، ويعمل على تمليس عملية تقليل التشويش في الصورة. في هذا المرشح يتم تبديل الشدة في كل مربع بكسل بمتوسط الشدة الموزون من قيم مربعات بكسل المحيطة، وبذلك يملس الصورة ويجعلها أدق وأقل حدة، وأعلى جودة.


- مرشح لابلاسيال
هو نوع آخر من مرشحات تحديد الحواف عن طريق إزالة الألوان ورسم الحواف.
- مرشح التآكل ومرشح التمدد
وهي مرشحات مورفولوجية أو تشكيلية تتم بناءً على الأشكال في الصورة.



واجهة جاهزة لتجريب بعض المرشحات
في حال أردت تجريب بعض المرشحات المذكورة ومرشحات
أخرى يمكنك ذلك دون الحاجة لكتابة أي كود!
واجهة setosa.io من تطوير Victor Powell تساعد على فهم الأنوية وعملية الالتفاف بتمثيل آني دون الحاجة لمعرفة المفاهيم والنصوص البرمجية المعقدة.

خاتمة
في هذا المقال، تعرفنا على ماهية المرشحات والأنوية الحسابية الالتفافية.
الأنوية الحسابية الالتفافية هي الأساس لبناء المرشحات. وتتكون من مصفوفات ذات أبعاد فردية.
يمكن عمل الكثير من التطبيقات بواسطة هذه المرشحات،مثل تعديل الصور وتجميلها بشكل ذكي واحترافي.
يوجد الكثير من المرشحات المطورة والأعلى ذكاءً لكن تعرفنا في هذا المقال على أساسيات المرشحات وأهم المرشحات الحسابية في مجال معالجة الصور في الذكاء الاصطناعي.
ملخص
- المرشح هو سلسلة من العمليات يطبق على الصورة يحتوي على أنوية التفافية ودوال.
- النواة هي الأساس للمرشح وهي عبارة عن مصفوفة فردية الابعاد.
- أشهر الأنوية الالتفافية هي نواة التطابق، ونواة التشويش، ونواة الشحذ.
- مرشح كاني هو أشهر المرشحات لرسم وتحديد الحواف.
- المرشحات تتنوع بين تحديد الحواف وتغيير الأشكال والتشويش والتوضيح.
- تطبيقات المرشحات متنوعة وكثيرة مثل مجال تعديل الصور بشكل ذكي وسريع.
- يمكن إنشاء وتطوير المرشحات عن طريق لغات البرمجة مثل بايثون ومكتبة اوبن سي في.
- لتجريب المرشحات وفهمها بشكل سهل ودون الحاجة للبرمجة، واجهة Setosa.io توفر هذه التجربة الفريدة.
المراجع
- https://docs.opencv.org/4.x/da/d22/tutorial_py_canny.html
- https://learnopencv.com/image-filtering-using-convolution-in-opencv/
- https://medium.com/@ianormy/convolution-filters-4971820e851f
- https://towardsdatascience.com/types-of-convolution-kernels-simplified-f040cb307c37
- https://www.di.univr.it/documenti/OccorrenzaIns/matdid/matdid666794.pdf
- https://sbme-tutorials.github.io/2018/cv/notes/4_week4.html
- https://www.isahit.com/blog/why-to-use-grayscale-conversion-during-image-processing#:~:text=It%20eliminates%20every%20form%20of,red%2C%20blue%20and%20green
- https://stackoverflow.com/questions/51167768/sobel-edge-detection-using-opencv
- https://www.tutorialspoint.com/opencv/opencv_dilation.htm
- https://www.tutorialspoint.com/opencv/opencv_bilateral_filter.htm